Mit Blackjack Team Basic Strategy Chart

Blackjack
Mit Blackjack Team Basic Strategy Chart Dealer Hits Soft 17

Contents

Mit Blackjack Chart. Mit blackjack chart online games casino free Blackjack Strategy Chart Mit revel rates atlantic city coushatta casino bus tripsWe will go through some of the best known and proven strategies of Blackjack game, which would definitely lower the house edge by about 2 percent.Learn how to read a blackjack strategy chart and find examples of a 6 deck black jack strategy charts.

Why the Blackjack Betting Strategy Matters

As the composition of the shoe changes, players are more or less likely to get blackjack based on the number of big cards left to be dealt out. It makes sense for players to bet large amounts when the odds are in their favor. The true count is what determines our advantage and ultimately the amount we should bet. The true count is fully explained in our blackjack card counting section.

Aug 01, 2019 Therefore, our basic strategy article won’t pay attention to these situations as they are considered to be part of a total-dependent blackjack strategy. The basic blackjack strategy chart will outline the best possible decision for those that don’t count cards. Growth of MIT blackjack: With the good response from the people the team started to grow and by the end of the year 1984 there were 35 players in the MIT blackjack team. Massar also called as Mr. M had got a chance to meet up with Bill Kaplan who also had a Blackjack team running successfully. Kaplan wanted to work together with the MIT.

The Kelly Criterion

The Kelly Criterion says that if a player knows his advantage then he should bet that percentage of his bankroll. For example, if the true count and the table rules indicate that the player has a 2 percent advantage and the bankroll is $2,500 then the bet should be 2 percent of $2,500 or $50. Many players do not have a $2,500 bankroll. As such, it is important to play at tables that have low enough minimums for players to capitalize when odds are favorable.

The World’s Greatest Blackjack Book does a nice job explaining the Kelly Criterion:

Trusting for now that you can gain an advantage with a counting system, the real question becomes: How should you bet in order to maximize your profits while minimizing your risk? Once again, the mathematicians have answered this one for us. According to Professor J. L. Kelly in 1956, the optimal betting method is to bet a percentage of your total bankroll that corresponds exactly to the percent advantage you have at any particular time. Professor Kelly and other scientists have proven both mathematically and in practice that this “Kelly Criterion” is the most profitable long-run method of wagering.
[The World’s Greatest Blackjack Book page 203]

MIT Betting Strategy

The old school MIT strategy is as follows when the count is +2 or more:
Amount to Bet = (True Count – 1) * Betting Unit

Using a table with a $5 minimum and a betting unit of $25, we have the following:

Count 0 or Less: bet $5
Count +1: bet $5
Count +2: bet $25
Count +3: bet $50

Bankroll Management

Most casual blackjack players have a smaller bankroll than the MIT team. As such, our betting strategy modifies their bet sizing table in order to reduce variance for small bankrolls.

Our Betting Strategy

Players bet the minimum when the true count is near 0 or less than 0.
We use a system where the betting unit matches the table minimum.

Here is our betting strategy on a $10 minimum table:

Count 0 or Less: bet $10
Count +1: bet $20
Count +2: bet $30
Count +3: bet $40
…
Count +x: bet 10*(x+1)

This betting strategy has less short term variance than the MIT betting strategy.

Hand Example

The true count is +2 and we’re sitting on a table with a $10 minimum. What should we bet for the next hand?

$30 is the answer based on our betting strategy above.

Another Hand Example

Blackjack

The true count is +3 and we’re sitting on a table with a $10 minimum. How much do we bet on the next hand?

Referencing our betting strategy above, we bet $40 on the next hand.

Introduction

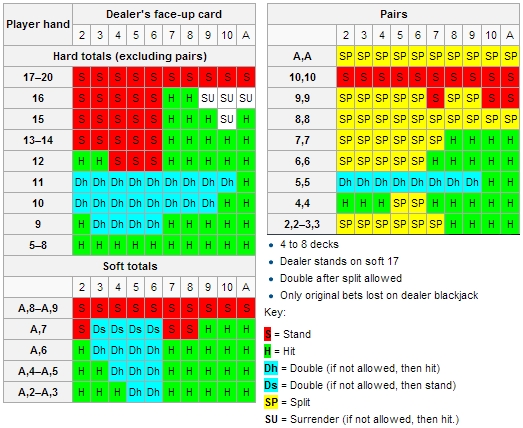
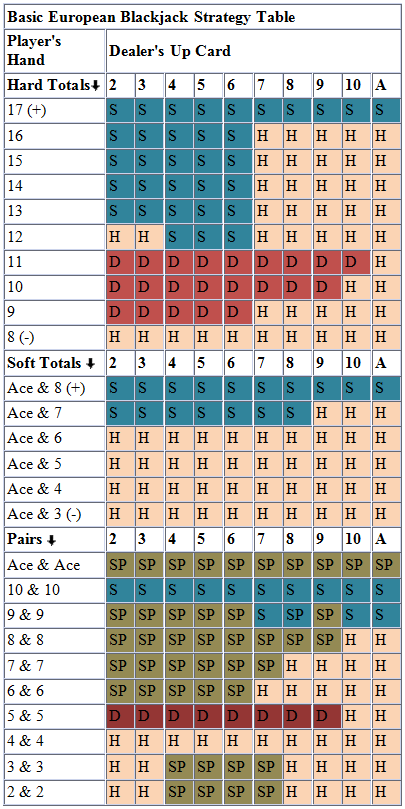
To use the basic strategy, look up your hand along the left vertical edge and the dealer's up card along the top. In both cases an A stands for ace. From top to bottom are the hard totals, soft totals, and splittable hands. There are two charts depending on whether the dealer hits or stands on soft 17.

Other basic strategy rules.

Never take insurance or 'even money.'
If there is no row for splitting (fives and tens), then look up your hand as a hard total (10 or 20).
If you can't split because of a limit on re-splitting, then look up your hand as a hard total.

If you play a mixture of six-deck games, some where the dealer hits a soft 17, and some where he stands, and you only wish to memorize one strategy, I would recommend you memorize the one where the dealer stands on soft 17. The cost in errors due to playing the wrong strategy is 2.3 times higher playing a stand on soft 17 game, with the hit on 17 strategy, than vise versa.